This series is inspired by my recent efforts to learn about applying deep learning in the music information retrieval field. I attended a two-week workshop on the same topic at Stanford’s Center for Computer Research in Music and Acoustics, which I highly recommend to anyone who is interested in AI + Music. This series is guided by Choi et al.’s 2018 paper, A Tutorial on Deep Learning for Music Information Retrieval.

It will consist of four parts: Background of Deep Learning, Audio Representations, Convolutional Neural Network, Recurrent Neural Network. This series is only a beginner’s guide.

My intent of creating this series is to break down this topic in a bullet point format for easy motivation and consumption.



Convolution

I struggled for a long time to understand what convolution means. Turns out it can be explained from different perspectives. Chris Olah has this amazing explanation of convolution from probability’s perspective.

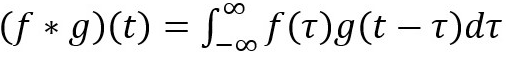
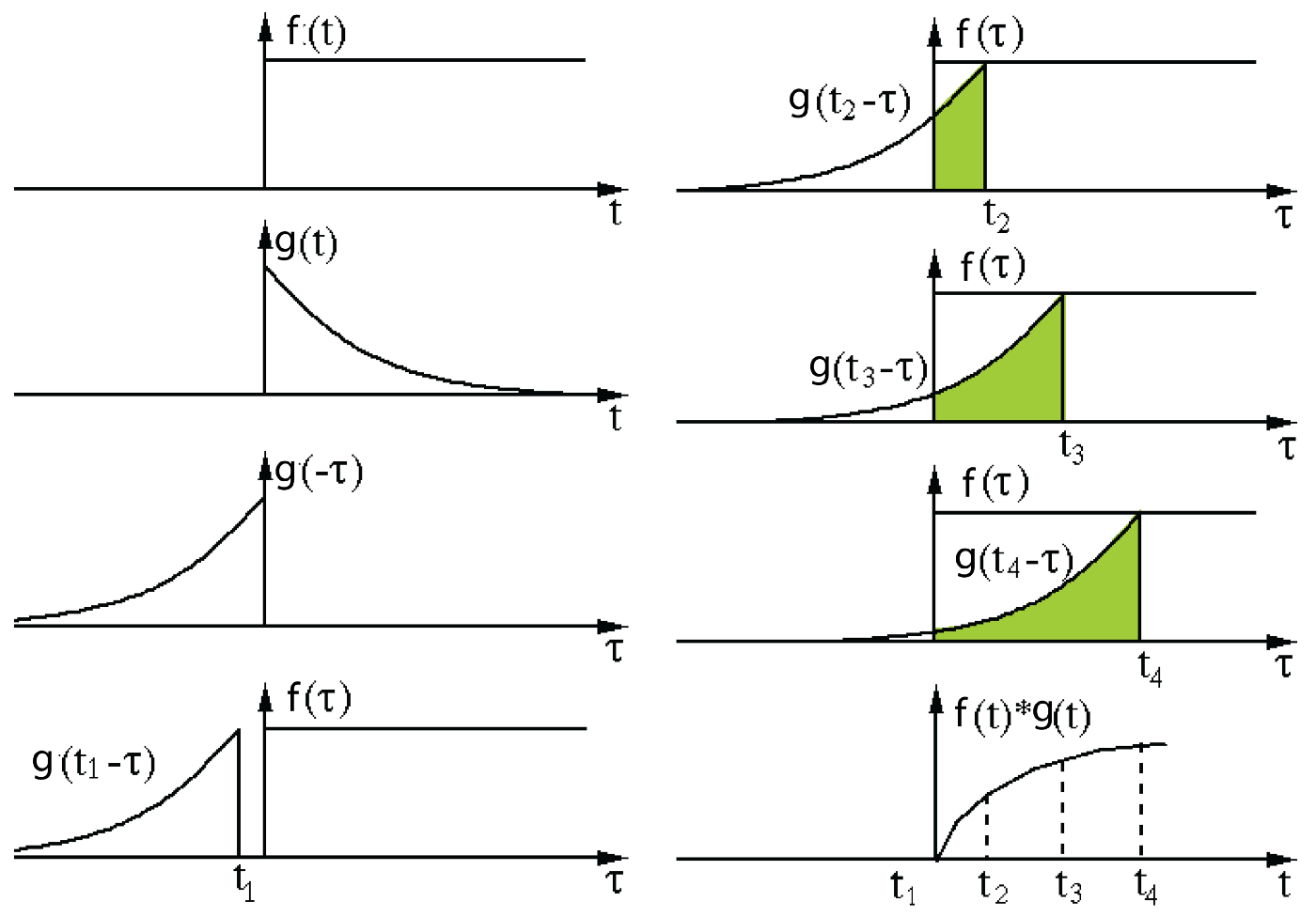
convolutions
Mathematical definition: t here can be treat as a constant that changes. So in the context of signal processing, it can be thought of filter g is reversed, and then slides along the horizontal axis. For every position, we calculate the area of the intersection between f and g. This area is the convolution value at the specific position. See the gif from convolution Wikipedia page.

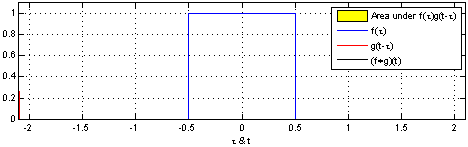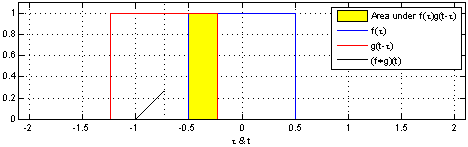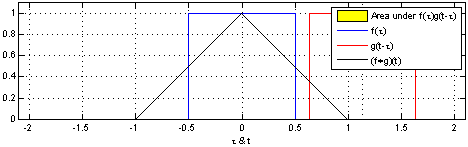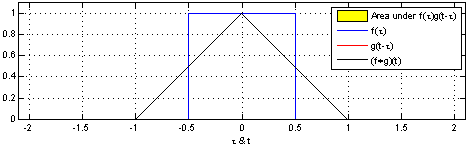
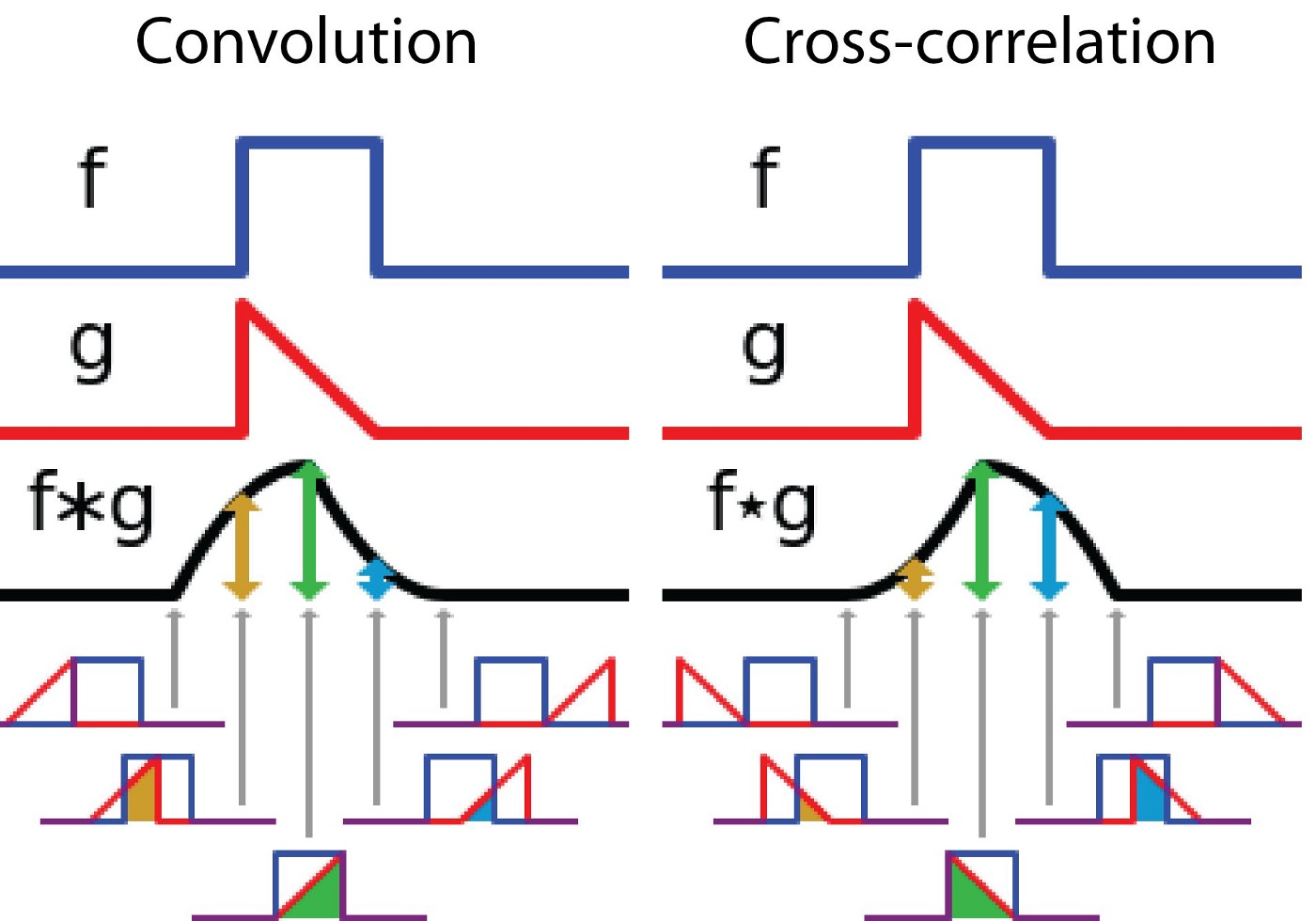
convolutions

convolutions
In convolutional neural networks, the filters are not reversed. It is technically called cross-correlation.

convolutions



How 2D Convolutional Network works with multiple channels

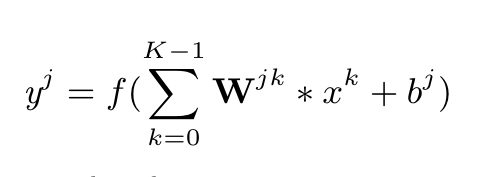
formula

  • Input: multiple channels of 2D arrays. in total K channels

  • Kernel: small 2D array of weights

    • 4D array for all the kernels in one layer, which means for all k and j: (h,l, K, J)

  • Filter: a collection of kernels

    • the number of kernels in a filter = the number of input channels = K

    • each channel will have one unique kernel to slide through

  • Output channels: equivalent to the neurons in that layer. in total J channels

    • 1 filter only yields 1 output channel

  • There’s only 1 bias term for each filter

Example input has 3 channels (K = 3), each channel is 5x5. Kernel is 3x3.

Step 1: Each unique kernel in a filter will go through each input channel and yield a processed version of that input channel. So we will get K unique kernels.

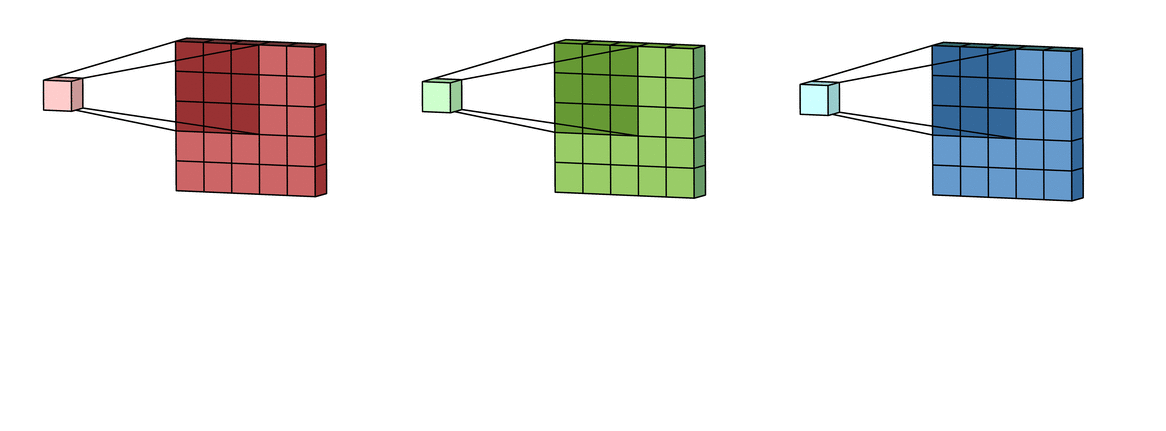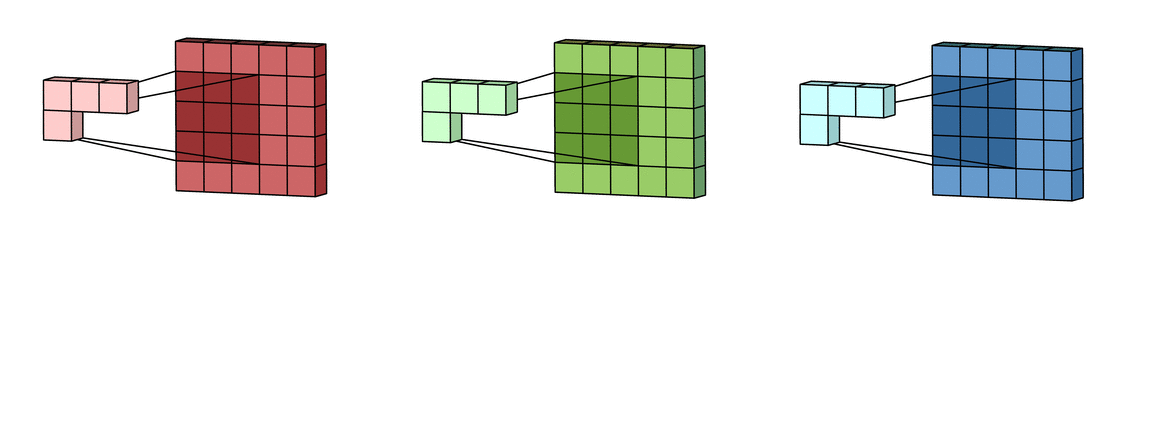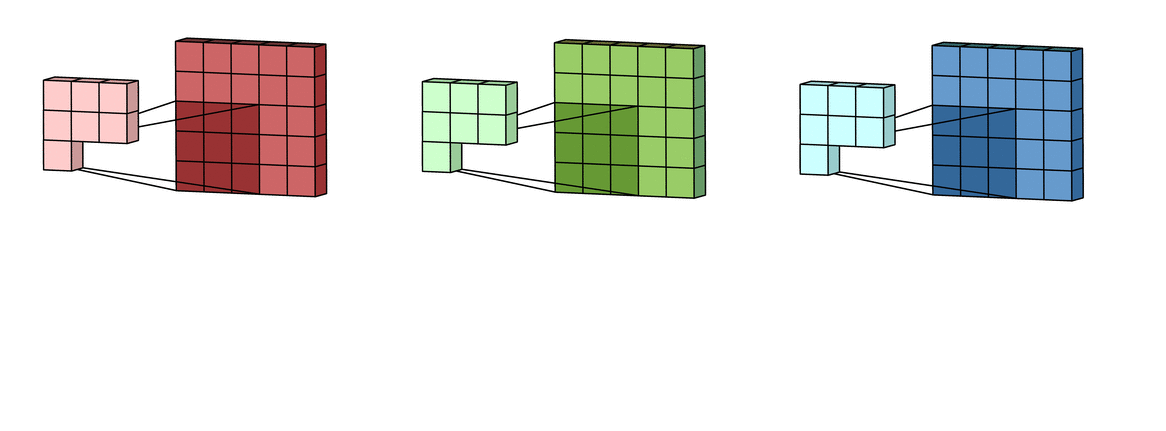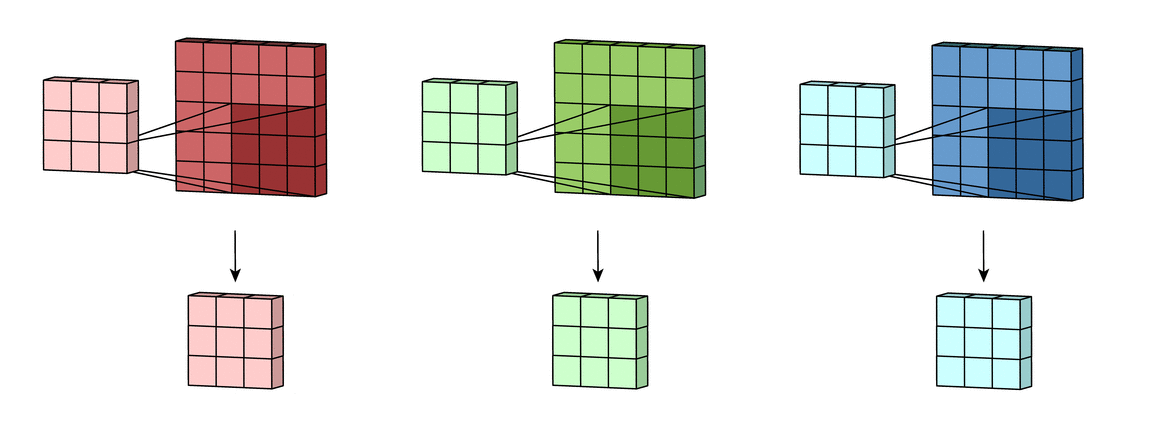CNN 1 Reference image is from Irhum Shafkat's Medium article.

Step 2: Sum over all the processed versions to get one output channel

CNN 2

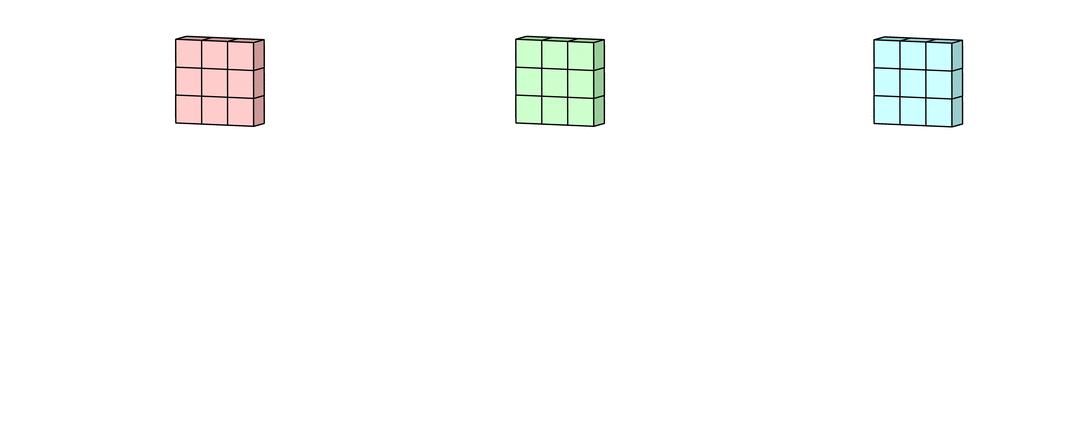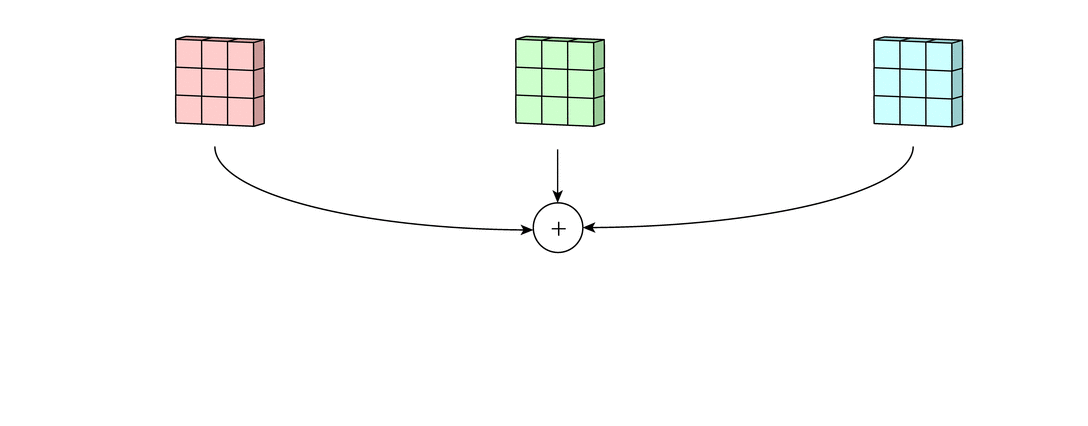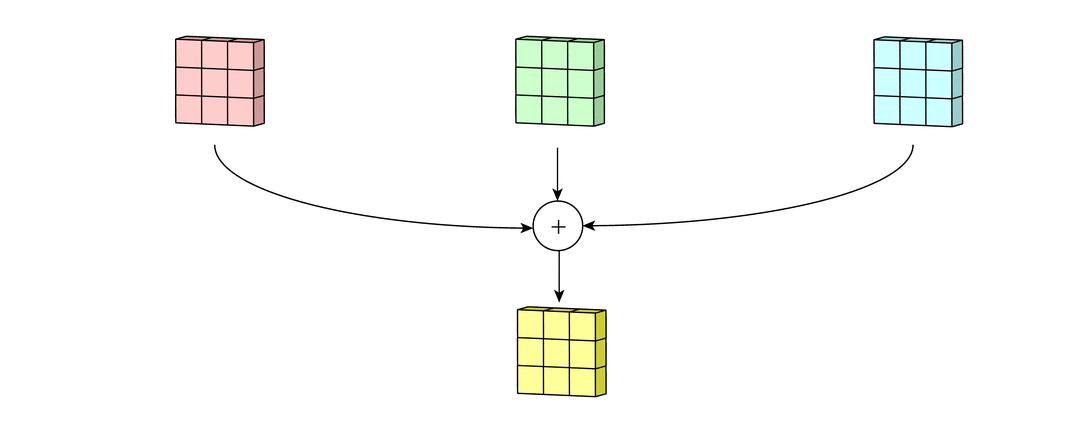
Step 3: Add in the bias term for this filter to get the final output channel. Note this will be yj

CNN 3

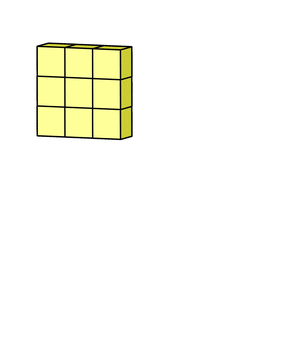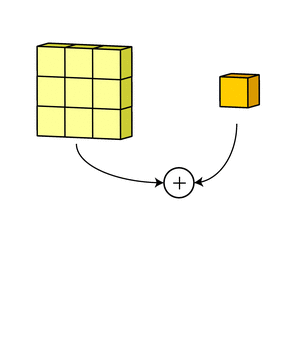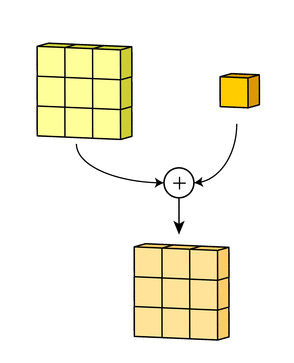
Subsampling:

Usually convolutional layers are used with pooling layers. For example, a maxpool.

  • Pooling layer reduces the size of feature maps by downsampling them with an operation.

    • Max function tests if there exists an activation in a local region, but discards the precise location of the activation

    • Average operation usually not used, but it is applied globally after the last convolutional layer to summarize the feature map activation on the whole area of input, when input size varies

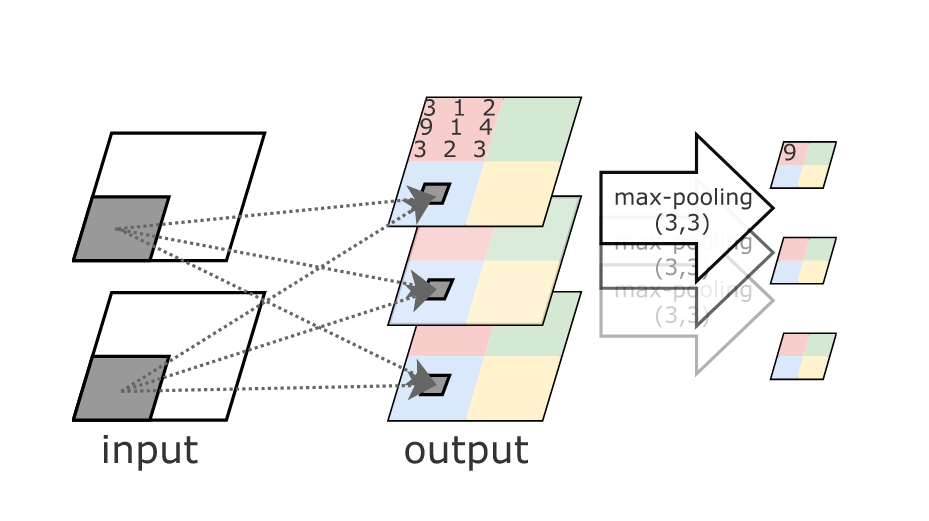
formula

CNN & Music

  • Example use cases where CNN could be used in music:

    • 1D convolutional kernel that learns fundamental frequencies from raw audio samples

    • Apply 2D convolutional layers to 2D time-frequency representations

  • Kernel size: determines maximum size of a component that the kernel can precisely capture in the layer

    • Not too small: should at least be big enough to capture the difference between the two patterns you are trying to capture

    • When the kernel is big, best to use it with a stacked convolution layers with subsamplings so that small distortions can be allowed. This is because kernel does not allow invariance in it.

  • CNN is shift invariant, which means the output will shift with the input but it stays otherwise unchanged. To put it plainly, a cat can be moved to another location of the image, but CNN will still be able to detect the cat.



Resources:

Kunlun Bai’s Medium article about different types of convolutions in CNNs here

Irhum Shafkat’s Medium article with awesome visualizations here

Chris Olah’s blog about CNNs here

GA Tech’s Polo Club of Data Science’s Interactive CNN learner in browser here